Introdução
Calcular porcentagens é uma habilidade essencial usada em vários aspectos da vida cotidiana, seja analisando dados financeiros, calculando descontos, determinando notas ou avaliando metas pessoais de condicionamento físico. O conceito de porcentagem representa uma parte de um todo, expressa como uma fração de 100. Isso facilita a compreensão de proporções e relacionamentos em diferentes contextos.
Neste guia abrangente, vamos nos aprofundar no que significa porcentagem, nas várias fórmulas para calculá-la, aplicações no mundo real e exemplos passo a passo. No final, você dominará a arte de calcular porcentagens, entenderá sua importância e se tornará adepto da aplicação do conhecimento em cenários práticos.
O que é porcentagem?
Porcentagem é uma maneira de expressar um número como uma fração de 100. O termo se origina da frase latina per centum, que significa “por cem”. Por exemplo, 50% significa 50 de cada 100 unidades, ou 1/2. Este método é amplamente utilizado porque simplifica comparações entre valores, independentemente de seus tamanhos absolutos.
As porcentagens são indicadas pelo símbolo %. A beleza das porcentagens está em sua versatilidade — elas são usadas em matemática, finanças, negócios, ciências e cenários cotidianos, como calcular gorjetas, impostos ou descontos.
Principais componentes de uma porcentagem
Antes de passarmos para as fórmulas, vamos esclarecer os três principais componentes envolvidos no cálculo de porcentagens:
Porcentagem (%): Um valor expresso em 100.
Parte ou valor: Uma porção específica do todo.
Todo ou total: A quantidade completa ou total sendo medida.
Fórmula básica de porcentagem
A fórmula básica para calcular uma porcentagem é:
Porcentagem=(Todo / Parte)×100
Esta fórmula ajuda a determinar qual porcentagem uma parte é de um todo.
Exemplo 1: Cálculo de porcentagem simples
Problema: Você obteve 45 pontos de 60 em um teste de matemática. Qual é sua pontuação percentual?
Solução:
Usando a fórmula:
Porcentagem=(60 / 45)×100
Porcentagem=0,75×100=75%
Então, sua pontuação é 75%.
Como calcular aumento e diminuição percentual
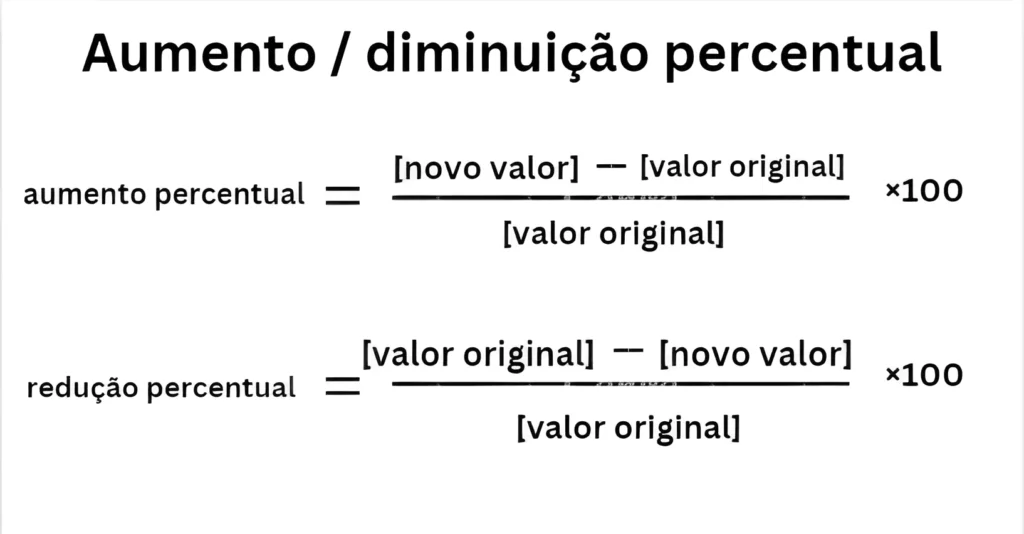
Uma das aplicações mais comuns de porcentagens é calcular aumento ou diminuição percentual, o que é útil para rastrear crescimento ou redução ao longo do tempo.
Fórmula de aumento percentual
Aumento percentual = (valor original / novo valor – valor original) × 100
Exemplo:
O preço de um produto aumenta de $ 50 para $ 60. Qual é o aumento percentual?
Solução:
Aumento percentual = (50 / 60−50) × 100
Aumento percentual = (50 / 10) × 100 = 20%
Então, o aumento percentual é de 20%.
Fórmula de redução percentual
Redução percentual = (valor original / valor original – novo valor) × 100
Exemplo:
Um telefone que originalmente custava US$ 800 agora está disponível por US$ 600. Qual é a redução percentual no preço?
Solução:
redução percentual=(800 / 800−600)×100
redução percentual=(800 / 200)×100=25%
A redução percentual é de 25%.
Cálculo de porcentagem reversa
Às vezes, você pode saber a porcentagem e o valor final, mas precisa calcular o valor original. Esse processo é chamado de cálculo de porcentagem reversa.
Fórmula de porcentagem reversa:
Preço original=(1±Porcentagem de alteração/100)Valor final
Use o sinal + para aumentos percentuais.
Use o sinal – para reduções percentuais.
Exemplo:
Uma TV é vendida por US$ 900 após um desconto de 10%. Qual era o preço original?
Solução:
Preço original=1−(10/100)900=0.9900=1000
O preço original era $ 1.000.
Encontrando uma parte dada uma porcentagem
Se você souber a porcentagem e o valor total, poderá encontrar a parte que corresponde a essa porcentagem. A fórmula é:
Parte=(100 por cento)×Todo
Parte=(10020)×300=0.2×300=60
Portanto, 20% de 300 é 60.
Aplicações de porcentagens no mundo real
Porcentagens são usadas em vários campos, incluindo:
Finanças e investimentos:
Taxas de juros sobre empréstimos ou contas de poupança são expressas em porcentagens.
Retornos do mercado de ações são medidos em aumentos ou diminuições percentuais.
Negócios e vendas:
Descontos são frequentemente expressos como porcentagens (por exemplo, 15% de desconto).
Margens de lucro e marcações são calculadas como porcentagens de custos.
Educação:
As notas dos exames são frequentemente convertidas em porcentagens.
Médias de notas (GPAs) são influenciadas por pontuações baseadas em porcentagens.
Saúde e condicionamento físico:
A porcentagem de gordura corporal é usada para medir os níveis de condicionamento físico.
Metas baseadas em porcentagem (por exemplo, “reduzir calorias
ingestão em 10%”) ajudam no planejamento de dietas.
Estatísticas e análise de dados:
Porcentagens são usadas para relatar resultados de pesquisas e descobertas de pesquisas.
Cálculos de probabilidade geralmente envolvem porcentagens.
Dicas práticas para cálculos de porcentagem
Converter frações em porcentagens: multiplique a fração por 100.
Exemplo:
3 / 4 =0,75×100=75%.
Converter decimais em porcentagens: multiplique o decimal por 100.
Exemplo:
0,35×100=35%.
Use matemática mental para cálculos rápidos:
10% de um número é simplesmente 1/10 dele.
1% é encontrado dividindo o número por 100.
Use uma calculadora para cálculos complexos: para números grandes ou porcentagens precisas, uma calculadora garante precisão.
Erros comuns a evitar
Esquecer de multiplicar por 100:
Ao calcular porcentagens, lembre-se sempre de multiplicar por 100 no final.
Misturar aumento e diminuição de porcentagem:
Use a fórmula correta com base no aumento ou na diminuição do valor.
Arredondamento muito cedo:
Evite arredondar valores intermediários até a etapa final para garantir precisão.
Conclusão
Entender como calcular porcentagens é uma habilidade de vida crucial que simplifica a comparação, o planejamento e a tomada de decisões. Esteja você trabalhando com dados financeiros, avaliando descontos ou monitorando o progresso em direção a objetivos pessoais, as porcentagens fornecem clareza e precisão. Ao dominar as fórmulas e praticar aplicações do mundo real, você pode lidar com confiança com problemas relacionados a porcentagens.
Lembre-se, a fórmula fundamental —Porcentagem=(Parte / Toda)×100— forma a base para cálculos mais avançados. Com a prática, calcular aumentos, diminuições e porcentagens reversas de porcentagens se tornará uma segunda natureza.
Armado com esse conhecimento, você agora está pronto para lidar com problemas de porcentagem em situações cotidianas, seja na escola, no trabalho ou na sua vida pessoal.
Para mais detalhes visite esta página https://porcentagemcalculadora.com/