Como calcular probabilidade usando porcentagens: um guia abrangente
Como calcular probabilidade com porcentagem..
Calcular probabilidade com porcentagens é uma habilidade essencial em estatística e tomada de decisão. Esse processo envolve converter porcentagens em probabilidades e aplicar princípios básicos da teoria da probabilidade. Nesta discussão detalhada, exploraremos o conceito de probabilidade, a relação entre porcentagens e probabilidades e os métodos passo a passo para calcular probabilidades usando porcentagens. Também abordaremos aplicações práticas, erros comuns e estratégias para interpretar resultados de probabilidade.
1. Compreendendo probabilidade e porcentagens
1.1 O que é probabilidade?
Probabilidade é a medida da probabilidade de um evento ocorrer, expressa como um número entre 0 e 1:
- Uma probabilidade de 0 significa que o evento é impossível.
- Uma probabilidade de 1 significa que o evento é certo.
1.2 O que são porcentagens?
Porcentagens representam uma parte de 100. Por exemplo, 50% significa metade de algo, 25% significa um quarto e assim por diante.
1.3 Relação entre probabilidade e porcentagens
Porcentagens e probabilidades estão intimamente relacionadas:
- Probabilidades podem ser convertidas em porcentagens multiplicando por 100.
- Porcentagens podem ser convertidas em probabilidades dividindo por 100.
Por exemplo:
- Uma chance de 60% de chuva se traduz em uma probabilidade de ( 0,6 ).
- Uma probabilidade de ( 0,3 ) é equivalente a uma probabilidade de 30%.
2. Fórmula básica para Como calcular probabilidade com porcentagem
A fórmula para calcular probabilidade com porcentagens é:
Probabilidade = Porcentagem / 100
Por outro lado, se você começar com uma probabilidade e quiser a
porcentagem = Probabilidade × 100
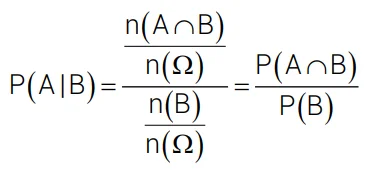
3. Tipos de cenários de probabilidade usando porcentagens
Existem vários cenários em que porcentagens são usadas para calcular probabilidades:
3.1 Probabilidade de evento único
Isso envolve a probabilidade de um evento ocorrer. Por exemplo:
- Qual é a probabilidade de selecionar aleatoriamente uma bolinha azul se 40% das bolinhas forem azuis?
3.2 Eventos combinados
Quando vários eventos estão envolvidos, as porcentagens podem ajudar a calcular:
- Eventos independentes: Eventos em que o resultado de um não afeta o outro.
- Eventos dependentes: Eventos em que o resultado de um afeta o outro.
3.3 Probabilidade complementar
A probabilidade de um evento não acontecer pode ser calculada como:
P(Noa’ A)=1−P(A)
Por exemplo, se houver 75% de chance de chuva, a probabilidade de não chover é
( 1 – 0,75 = 0,25 ) ou 25%.
4. Guia passo a passo para calcular probabilidade com porcentagens
Etapa 1: converter a porcentagem em probabilidade
Para calcular a probabilidade, divida a porcentagem fornecida por 100. Por exemplo:
- Uma chance de 70% se converte em ( 70 \div 100 = 0,7 ).
Etapa 2: identificar o número total de resultados
Determine o número total de resultados possíveis para o evento. Por exemplo:
- Em uma loteria com 100 bilhetes, há 100 resultados possíveis.
Etapa 3: determinar resultados favoráveis
Identifique quantos resultados correspondem ao evento em questão. Por exemplo:
- Se 20 bilhetes ganharem um prêmio, há 20 resultados favoráveis.
Etapa 4: Aplique as regras de probabilidade
Use a fórmula de probabilidade:
P(Evento) = Resultados favoráveis / Resultados totais
Etapa 5: Converta de volta para porcentagem, se necessário
Se necessário, multiplique a probabilidade por 100 para expressá-la como uma porcentagem.
5. Exemplos práticos
5.1 Exemplo de evento único
Pergunta: Qual é a probabilidade de escolher uma bola vermelha de uma sacola se 30% das bolas forem vermelhas?
Solução:
- Converta porcentagem em probabilidade: ( 30 \div 100 = 0,3 ).
- A probabilidade é 0,3 ou 30%.
5.2 Exemplo de eventos combinados
Pergunta: Uma moeda é lançada e um dado é lançado. Qual é a probabilidade de obter cara e rolar um 6?
Solução:
- Probabilidade de cara: ( 50\% = 0,5 ).
- Probabilidade de rolar um 6: ( \frac{1}{6} \approx 0,1667 ).
- Probabilidade de ambos: ( 0,5 \vezes 0,1667 = 0,0833 ).
- Converter para porcentagem: ( 0,0833 \vezes 100 = 8,33\% ).
5.3 Exemplo de probabilidade complementar
Pergunta: Se há 65% de chance de um produto ser defeituoso, qual é a probabilidade de ele não ser defeituoso?
Solução:
- Probabilidade de não ser defeituoso: ( 1 – \frac{65}{100} = 0,35 ).
- A probabilidade é 0,35 ou 35%.
6. Aplicações reais de probabilidade usando porcentagens
6.1 Negócios e finanças
- Avaliar riscos de mercado (por exemplo, uma chance de 20% de queda nos preços das ações).
- Prever crescimento de vendas (por exemplo, uma probabilidade de 75% de atingir metas).
6.2 Educação
- Calcular a probabilidade de passar em um exame com base no desempenho nos estudos.
- Analisar probabilidades de frequência em salas de aula.
6.3 Assistência médica
Avaliar a probabilidade de sucesso do tratamento.
Estimar probabilidades de risco de doenças em populações.
6.4 Jogos e esportes
Prever resultados de jogos com base em estatísticas de equipe.
Calcular probabilidades em loterias ou cenários de apostas.
Ferramentas para cálculos de probabilidade
7.1 Cálculos manuais
Métodos manuais usando aritmética básica são suficientes para cenários simples.
7.2 Planilhas
Ferramentas como o Excel simplificam os cálculos, especialmente para eventos múltiplos. Use fórmulas como:
=Porcentagem/100=1 – Probabilidade
7.3 Calculadoras de probabilidade
Calculadoras on-line podem calcular probabilidades, especialmente para eventos complexos, como combinações ou permutações.
Erros comuns no cálculo de probabilidade com porcentagens
8.1 Interpretação incorreta de porcentagens
Deixar de converter porcentagens em probabilidades (ou vice-versa) leva a erros.
8.2 Ignorando independência/dependência
Assumindo incorretamente que eventos são independentes quando não são.
8.3 Negligenciando resultados totais
Contar incorretamente os resultados totais possíveis distorce os resultados de probabilidade.
Interpretando resultados de probabilidade
9.1 Probabilidades altas vs. baixas
Uma probabilidade alta (próxima de 1 ou 100%) sugere que o evento é provável.
Uma probabilidade baixa (próxima de 0 ou 0%) sugere que o evento é improvável.
9.2 Usando probabilidades para tomada de decisão
As probabilidades podem orientar decisões, mas devem ser interpretadas juntamente com outros fatores como risco, custo e consequências.
Conclusão
Calcular probabilidade usando porcentagens é uma habilidade fundamental que faz a ponte entre a tomada de decisão cotidiana e a análise estatística complexa. Ao entender a relação entre porcentagens e probabilidades, aplicar as fórmulas corretas e interpretar os resultados de forma eficaz, você pode obter insights valiosos sobre vários cenários do mundo real. Seja prevendo resultados, avaliando riscos ou tomando decisões estratégicas, os cálculos de probabilidade fornecem uma abordagem estruturada para navegar na incerteza. Para mais informações, clique aqui….